



Next: A regra G-INV
Up: Métodos de prova para
Previous: Métodos de prova para
Na figura 4.1 é apresentada a regra B-INV (basic
invariance) que permite provar que uma fórmula de estado p é um
invariante de um programa P.
Figure 4.1:
Regra B-INV
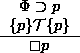 |
A primeira premissa obriga que a condição inicial 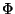 implique p,
i.é, p tem que ser válido nos estados iniciais do programa. Para
entender a segunda regra são necessários alguns conceitos adicionais.
Primeiro é preciso relembrar que
implique p,
i.é, p tem que ser válido nos estados iniciais do programa. Para
entender a segunda regra são necessários alguns conceitos adicionais.
Primeiro é preciso relembrar que
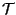 representa o conjunto
de todas as transições de um programa. Temos também a seguinte
equivalência:
representa o conjunto
de todas as transições de um programa. Temos também a seguinte
equivalência:
Esta equivalência implica que a segunda premissa corresponda não a uma
fórmula lógica, mas a um conjunto de fórmulas, uma por cada transição
existente no FTS correspondente ao programa. Finalmente temos que
onde 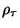 corresponde à fórmula lógica que caracteriza a transição
corresponde à fórmula lógica que caracteriza a transição
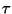 (ver tabela 3.1) e p' é a fórmula que se obtem
substituindo em p todas as ocorrências de variáveis livres pelas
respectivas versões linha. Dadas estas definições verifica-se que o
objectivo da segunda premissa consiste em verificar que a validade de
p é preservada por todas as transições.
(ver tabela 3.1) e p' é a fórmula que se obtem
substituindo em p todas as ocorrências de variáveis livres pelas
respectivas versões linha. Dadas estas definições verifica-se que o
objectivo da segunda premissa consiste em verificar que a validade de
p é preservada por todas as transições.
Note-se que a validade da fórmula temporal 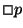 é verificada à
custa da validade de um conjunto de fórmulas de estado não temporais.
é verificada à
custa da validade de um conjunto de fórmulas de estado não temporais.
Como exemplo da utilização desta regra considere que se pretendia
provar, para o programa da figura 4.2, a validade da
fórmula
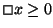 .
Neste caso,
.
Neste caso,
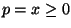 e, sendo uma fórmula
sem operadores temporais, podemos usar a regra B-INV para
provar a sua validade.
e, sendo uma fórmula
sem operadores temporais, podemos usar a regra B-INV para
provar a sua validade.
Figure 4.2:
Programa sequencial que soma 2 unidades
local x:int where x=0
l0: x := x+2;
l1:
|
A condição inicial 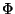 deste programa é
deste programa é
enquanto que a fórmula que caracteriza a sua única transição é
definida por
Começando pela primeira premisa
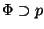 temos
temos
que é trivialmente válida. Como só temos uma transição a segunda
premissa só dá origem à propriedade
que simplifica para
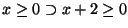 que também é trivialmente
válida. Pela regra B-INV concluimos que
que também é trivialmente
válida. Pela regra B-INV concluimos que
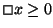 é
P-válida para o programa da figura 4.2.
é
P-válida para o programa da figura 4.2.




Next: A regra G-INV
Up: Métodos de prova para
Previous: Métodos de prova para
1999-05-25
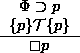
![]() implique p,
i.é, p tem que ser válido nos estados iniciais do programa. Para
entender a segunda regra são necessários alguns conceitos adicionais.
Primeiro é preciso relembrar que
implique p,
i.é, p tem que ser válido nos estados iniciais do programa. Para
entender a segunda regra são necessários alguns conceitos adicionais.
Primeiro é preciso relembrar que
![]() representa o conjunto
de todas as transições de um programa. Temos também a seguinte
equivalência:
representa o conjunto
de todas as transições de um programa. Temos também a seguinte
equivalência:
![]() é verificada à
custa da validade de um conjunto de fórmulas de estado não temporais.
é verificada à
custa da validade de um conjunto de fórmulas de estado não temporais.
![]() .
Neste caso,
.
Neste caso,
![]() e, sendo uma fórmula
sem operadores temporais, podemos usar a regra B-INV para
provar a sua validade.
e, sendo uma fórmula
sem operadores temporais, podemos usar a regra B-INV para
provar a sua validade.
![]() deste programa é
deste programa é