



Next: Pequeno caso de estudo
Up: Especificação de propriedades temporais
Previous: Estrutura de um ficheiro
As fórmulas da lógica temporal linear podem ser agrupadas em classes
de acordo com o seu poder expressivo. Nas fórmulas seguintes prepresenta uma fórmula temporal sobre o passado2.1.
Podemos definir as seguintes classes de fórmulas temporais,
caracterizadas pelos seus operadores mais externos:
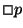 .
Proriedade de segurança ou invariância. Impõe que p se verifique sempre durante a execução do programa.
.
Proriedade de segurança ou invariância. Impõe que p se verifique sempre durante a execução do programa.
-
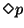 .
Propriedade de animação ou garantia. Garante que
p se verificará algures no furuto.
.
Propriedade de animação ou garantia. Garante que
p se verificará algures no furuto.
-
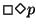 .
Propriedade de resposta. Indica que p ocorre um número infinito de vezes durante a execução do programa.
.
Propriedade de resposta. Indica que p ocorre um número infinito de vezes durante a execução do programa.
-
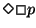 .
Propriedade de persistência. Garante que p será sempre válida a partir de um determinado instante de tempo no
futuro.
.
Propriedade de persistência. Garante que p será sempre válida a partir de um determinado instante de tempo no
futuro.
A seguir apresentamos alguns exemplos de fórmulas temporais e o
respectivo significado informal (p, q e r são fórmulas de
estado):
-
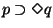 .
Se p se verificar no início da execução
então q será eventualmente verdadade. Propriedade de animação.
.
Se p se verificar no início da execução
então q será eventualmente verdadade. Propriedade de animação.
-
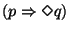 .
Qualquer estado onde p se verifique
coincide ou é seguido por um estado onde q também se verifica.
Propriedade de resposta.
.
Qualquer estado onde p se verifique
coincide ou é seguido por um estado onde q também se verifica.
Propriedade de resposta.
-
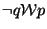 .
O ocorrência de q deve ser antecedida pela
ocorrência de p. Propriedade de segurança.
.
O ocorrência de q deve ser antecedida pela
ocorrência de p. Propriedade de segurança.
-
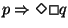 .
Um estado onde se verifique p é
eventualmente seguido de um estado a partir do qual q é sempre
verdade. Propriedade de persistência.
.
Um estado onde se verifique p é
eventualmente seguido de um estado a partir do qual q é sempre
verdade. Propriedade de persistência.
-
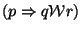 .
A ocorrência de p despoleta uma
sequência de estados onde q se verifica, eventualmente terminada
pela ocorrência de r.
.
A ocorrência de p despoleta uma
sequência de estados onde q se verifica, eventualmente terminada
pela ocorrência de r.
-
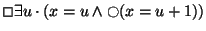 .
Nesta fórmula
u é uma variável rígida e x uma variável flexível e o seu
significado é o seguinte: o valor de x é incrementado de uma
unidade em todos os estados.
.
Nesta fórmula
u é uma variável rígida e x uma variável flexível e o seu
significado é o seguinte: o valor de x é incrementado de uma
unidade em todos os estados.
-
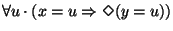 .
Nesta fórmula u é uma
variável rígida e x e y são variáveis flexíveis e o seu
significado é o seguinte: qualquer valor que x possa assumir é
eventualmente assumido por y.
.
Nesta fórmula u é uma
variável rígida e x e y são variáveis flexíveis e o seu
significado é o seguinte: qualquer valor que x possa assumir é
eventualmente assumido por y.




Next: Pequeno caso de estudo
Up: Especificação de propriedades temporais
Previous: Estrutura de um ficheiro
1999-05-25